Answer:
7.40%
Step-by-step explanation:
The coupon rate of the bond can be calculated as follows
Formula:
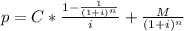
DATA
M = $1000
n = 22.5 *2 =45 semi-annual periods,
i = 6.9%/2 = 3.45% (semi-annually)
P = $1,057
Solution
1057 =
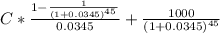
1057 = C * 22.69 + 217.33
839.67 + C * 22.69
C = $37.01 This is a semi-annual coupon
Annual Coupon = 2 * $37.01 = $74.02
Annual Coupon Rate = 7.40%