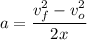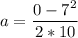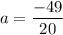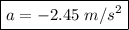Question

A car is traveling in a straight line path at a maximum speed of 7.00 m/s. The driver of the vehicle applies the brakes bringing the car to a stop after traveling 10.0 m. What is the magnitude of the car's acceleration to the nearest hundredths place?

Answer 1

`a=-2.45\ m/s^2`

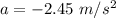
Step-by-step explanation:

An object is traveling at constant acceleration if its changes in speed are constant at the same intervals of time.

The acceleration can be calculated as follows:

`\displaystyle a=(v_f-v_o)/(t)`

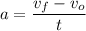
Where vo is the initial speed, vf the final speed and t is the time.

The acceleration and the distance x are related through the following equation:

`v_f^2=v_o^2+2.a.x`

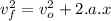
The car has an initial speed of vo=7 m/s when the driver stops the car (vf=0) after traveling x=10 m.

The acceleration can be calculated by solving the last equation for a:

`\displaystyle a=(v_f^2-v_o^2)/(2x)`

`\displaystyle a=(0-7^2)/(2*10)`

`\displaystyle a=(-49)/(20)`

`\boxed{a=-2.45\ m/s^2}`