Question

A man and a woman start from the same point. The man walks S60°E at 1.3 m/sec. The woman

walks south at 1.6 m/sec. At what rate is the distance between the man and woman changing
after 35 minutes?​

Answer 1

The distance between the man and woman is changing at the rate of 1.5 m/sec.

Explanation:

Speed =
`(distance)/(time)`

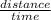
⇒ distance = speed x time

After 35 minutes (2100 seconds) ,

the man has walked a distance = 1.3 x 2100

= 2730 m

After 35 minutes, the woman has walked a distance = 1.6 x 2100

= 3360 m

The sketch of the displacement of the man and woman forms a triangle with an included angle. Applying the cosine rule, we have:

`c^(2)` =
`a^(2)` +
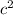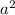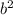`b^(2)` - 2abCos θ

=
`3360^(2)` +
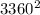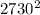`2730^(2)` - 2 x 3360 x 2730 x Cos
`60^(o)`

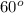
= 11289600 + 7452900 - 18345600(0.5)

= 18742500 - 9172800

= 9569700

c =
`√(9569700)`

= 3093.5 m

The distance between the man and woman at 35 minutes is 3093.5 m.

The distance between the man and woman is changing at the rate =
`(3093.5)/(2100)`

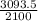
= 1.4731

= 1.5 m/sec

The distance between the man and woman is changing at the rate of 1.5 m/sec.