Question

MULTIPLE CHOICE CALCULUS

1) An object moves along a line so that its position at time t is s(t) = t^4 - 6t^3 - 2t - 1.

At what time t is the acceleration of the object zero?

A. at 3 only

B. at 0 and 3 only

C. at 0 only

D. at 1 only

2) If f(x) = e^x (sin x + cos x), then f'(x) =

A. 2e^x (cos x + sin x)

B. e^x cos x

C. e^x (cos^2x - sin^2x)

D. 2e^x cos x

Answer 1

1) B. at 0 and 3 only

2) D. 2eˣcosx

General Formulas and Concepts:

Pre-Algebra

Order of Operations: BPEMDAS

1. Brackets
2. Parenthesis
3. Exponents
4. Multiplication
5. Division
6. Addition
7. Subtraction

• Left to Right

Algebra I

• Terms/Coefficients
• Factoring
• Quadratics

Calculus

Derivatives

Derivative Notation

Derivative of a constant is 0

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Derivative Property [Addition/Subtraction]:
`\displaystyle (d)/(dx)[f(x) + g(x)] = (d)/(dx)[f(x)] + (d)/(dx)[g(x)]`

Derivative Rule [Product Rule]:
`\displaystyle (d)/(dx) [f(x)g(x)]=f'(x)g(x) + g'(x)f(x)`

Trig Derivative:
`\displaystyle (d)/(dx)[sinu] = u'cosu`

Trig Derivative:
`\displaystyle (d)/(dx)[cosu] = -u'sinu`

eˣ Derivative:
`\displaystyle (d)/(dx) [e^u]=e^u \cdot u'`

Explanation:

*Note:

Velocity is the derivative of position.

Acceleration is the derivative of velocity.

Question 1

Step 1: Define

s(t) = t⁴ - 6t³ - 2t - 1

Step 2: Differentiate

1. [Velocity] Basic Power Rule: s'(t) = 4 · t⁴⁻¹ - 3 · 6t³⁻¹ - 1 · 2t¹⁻¹
2. [Velocity] Simplify: v(t) = 4t³ - 18t² - 2
3. [Acceleration] Basic Power Rule: v'(t) = 3 · 4t³⁻¹ - 2 · 18t²⁻¹
4. [Acceleration] Simplify: a(t) = 12t² - 36t

Step 3: Solve

1. [Acceleration] Set up: 12t² - 36t = 0
2. [Time] Factor: 12t(t - 3) = 0
3. [Time] Identify: t = 0, 3

Question 2

Step 1: Define

f(x) = eˣ(sinx + cosx)

Step 2: Differentiate

1. [Derivative] Product Rule:
   `\displaystyle f'(x) = (d)/(dx)[e^x](sinx + cosx) + e^x(d)/(dx)[sinx + cosx]`
2. [Derivative] Rewrite [Derivative Property - Addition]:
   `\displaystyle f'(x) = (d)/(dx)[e^x](sinx + cosx) + e^x((d)/(dx)[sinx] + (d)/(dx)[cosx])`
3. [Derivative] eˣ Derivative:
   `\displaystyle f'(x) = e^x(sinx + cosx) + e^x((d)/(dx)[sinx] + (d)/(dx)[cosx])`
4. [Derivative] Trig Derivatives:
   `\displaystyle f'(x) = e^x(sinx + cosx) + e^x(cosx - sinx)`
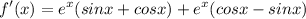
5. [Derivative] Factor:
   `\displaystyle f'(x) = e^x[(sinx + cosx) + (cosx - sinx)]`
6. [Derivative] Combine like terms:
   `\displaystyle f'(x) = e^x[2cosx]`
7. [Derivative] Multiply:
   `\displaystyle f'(x) = 2e^xcosx`

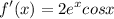
Topic: AP Calculus AB/BC (Calculus I/II)

Unit: Derivatives

Book: College Calculus 10e