Question

Help

Save & Exit
Submit
Rank the following elements in order from least to most number of moles of atoms in a 10.0 g sample: Sn, Si, Se, S

Answer 1

`\rm Sn`,
`\rm Se`,
`\rm S`,
`\rm Si`.

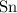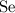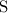Step-by-step explanation:

The relative atomic mass of an element is numerically equal to the mass (in grams) of one mole of its atoms. This quantity can help estimate the number of moles of atoms in each of these four
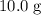`10.0\; \rm g` samples.

Look up the relative atomic mass for each of these four elements (on a modern periodic table.)

• 
  `\rm Si`:
  `28.085`.
• 
  `\rm S`:
  `32.06`.
• 
  `\rm Se`:
  `78.971`.
• 
  `\rm Sn`:
  `118.710`.

The relative atomic mass of
`\rm Si` is (approximately)
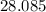`28.085`. Therefore, the each mole of silicon atoms would have a mass of approximately
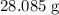`28.085\; \rm g`. How many moles of silicon atoms would there be in a
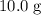`10.0\; \rm g` sample?

Given:

• 
  `m(\rm Si) = 10.0\; \rm g`.
• 
  `M(\mathrm{Si}) = 28.085\; \rm g \cdot mol^(-1)`.

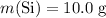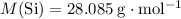Number of mole of silicon atoms in the sample:
`\displaystyle n(\mathrm{Si}) = \frac{m(\mathrm{Si})}{M(\mathrm{Si})} = (10.0\; \rm g)/(28.085\; \rm g \cdot mol^(-1))\approx 0.356\; \rm mol`.

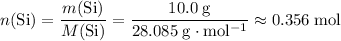Similarly:

`\displaystyle n(\mathrm{S}) = \frac{m(\mathrm{S})}{M(\mathrm{S})} = (10.0\; \rm g)/(32.06\; \rm g \cdot mol^(-1))\approx 0.312\; \rm mol`.

`\displaystyle n(\mathrm{Se}) = \frac{m(\mathrm{Se})}{M(\mathrm{Se})} = (10.0\; \rm g)/(78.971\; \rm g \cdot mol^(-1))\approx 0.127\; \rm mol`.

`\displaystyle n(\mathrm{Sn}) = \frac{m(\mathrm{Sn})}{M(\mathrm{Sn})} = (10.0\; \rm g)/(118.710\; \rm g \cdot mol^(-1))\approx 0.0842\; \rm mol`.

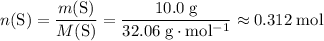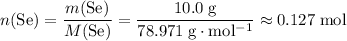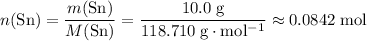Therefore, among these
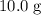`10.0\; \rm g` samples:

`n(\mathrm{Sn}) < n(\mathrm{Se}) < n(\mathrm{S}) < n(\mathrm{Si})`.

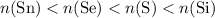It is not a coincidence that among these four samples, the one with the fewest number of atoms corresponds to the element with the largest relative atomic mass.

Consider two elements, with molar mass
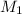`M_1` and
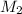`M_2` each. Assume that
`n_1` moles and
`n_2` moles of atoms of each element were selected, such that the mass of both samples is
`m`. That is:

`m = n_1\cdot M_1`.

`m = n_2\cdot M_2`.

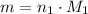Equate the right-hand side of these two equations:

`n_1 \cdot M_1 = n_2\cdot M_2`.

`\displaystyle (n_1)/(n_2) = (M_2)/(M_1) = (1/M_1)/(1/M_2)`.

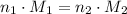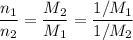In other words, the number of moles atoms in two equal-mass samples of two elements is inversely proportional to the molar mass of the two elements (and hence inversely proportional to the formula mass of the two elements.) That explains why in this question, the sample containing the smallest number of atoms corresponds to element with the largest relative atomic mass among those four elements.