Answer:
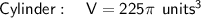
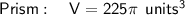
The volumes of the figures are the same.
Explanation:
Formulae
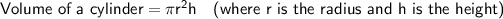
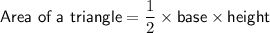
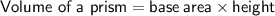
Volume of the cylinder
Given:
Substitute the given values into the formula and solve for V:
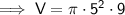
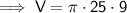

Volume of the triangular prism
Given values of triangular base:
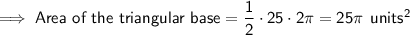
Given values of prism:
- Area of base = 25π
- Height = 9
Substitute the given values into the formula and solve for V:
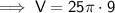

Conclusion
The volumes of the figures are the same.