Question

Mathew is a financial analyst for a surf board company. He has found an equation for the revenue of selling t-shirts with the company logo to be r= -3p^2 + 60p +1060, where p is the price of the company’s product. What should he use to determine the price of maximum sales?

Answer 1

Answer: The price of maximum sales is $160

Explanation:

This question requires you to find the vertex of this equation. The vertex of a parabola is the point where the parabola crosses its axis of symmetry.

since the coefficient of the
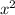`x^2` term is negative, the vertex will be the highest point on the graph.

this quadratic equation is in standard form:
`y = ax^2+bx+c`.

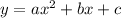From this, we can derive:

`a = -3`

`b = 60`

`c = 1060`

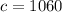
First, determine the axis of symmetry (
`p` is the variable for the horizontal axis (
`x`) in this instance). This will be our x-coordinate of the vertex.

`p = (-b)/(2a)`

`p = (-(60))/(2(-3))`

`p = (-60)/(-6)`

`p=10`

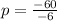
Then, substitute the axis of symmetry into the function to find the y coordinate of the axis of symmetry. r stands for the variable for the vertical axis in this instance. This will be our y-coordinate of the vertex.

`r = -3(10)^2+60(10)+1060`

`r = 160`

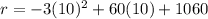
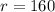
As we have determined both the x and y coordinate of the vertex for this equation, we can determine that the maximum point is at
`(10, 160)`.

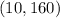the maximum price (
`r`) is 160