Question

A triangle has sides with lengths of 31 feet, 72 feet, and 78 feet. Is it a right triangle?

yes
no

Answer 1

Answer: No

=========================================================

Step-by-step explanation:

We have a triangle with these side lengths

• a = 31
• b = 72
• c = 78

The order of 'a' and b doesn't matter, but we must have c as the largest value. Usually a,b,c are in ascending order.

Plug those values into the formula for the pythagorean theorem. If we get the same thing on both sides, then we have a right triangle.

`a^2 + b^2 = c^2\\\\31^2 + 72^2 = 78^2\\\\961+5184 = 6084\\\\6145 = 6084\\\\`

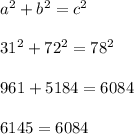
We have a false statement at the end, which means the original equation is false for those a,b,c values.

Therefore, we do not have a right triangle.

Instead, this triangle is acute since the
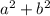`a^2+b^2` side is larger than the
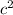`c^2` side

---------------

Rules to have in your notebook or on a reference sheet:

`\text{If }a^2 + b^2 = c^2 \text{ then it is a right triangle}\\\\\text{If }a^2 + b^2 > c^2 \text{ then the triangle is acute}\\\\\text{If }a^2 + b^2 < c^2 \text{ then the triangle is obtuse}\\\\`

For more information, check out the converse of the pythagorean theorem.