Question

PLZ HELP, BEST ANSWER GETS BRAINLLEST!

Determine the two closest integers for each irrational number.
the square root of 19
the square root of 50
the square root of 117

Answer 1

Answers:

• a) 4 and 5
• b) 7 and 8
• c) 10 and 11

=====================================================

Work Shown:

List out the perfect squares

{1,4,9,16,25,36,49,64,81,100,121}

We stop once we reach 117 or just a bit higher.

---------------------------

Then notice that

`16 < 19 < 25 \ ... \ \text{19 between the squares 16 and 25}\\\\√(16) < √(19) < √(25) \ ... \ \text{ apply square root to all sides}\\\\4 < √(19) < 5`

Which shows
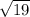`√(19)` is between 4 and 5. Therefore, the two closest integers to
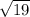`√(19)` are 4 and 5.

---------------------------

We follow the same steps for
`√(50)`

So,

`49 < 50 < 64\\\\√(49) < √(50) < √(64)\\\\7 < √(50) < 8`

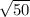
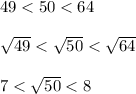
So the square root of 50 is between 7 and 8.

---------------------------

And finally,

`100 < 117 < 121\\\\√(100) < √(117) < √(121)\\\\10 < √(117) < 11`

---------------------------

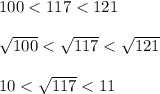
Using a calculator, we find that

`√(19) \approx 4.36`

`√(50) \approx 7.07`

`√(117) \approx 10.82`

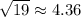
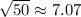
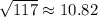
which helps confirm our answers.