Question

A bacteria that starts with 3 cells increases by 15% every hour.

Write an exponential growth equation that models the situation



How many bacteria cells will there be in 13 hours?

Answer 1

The answer to your problem in 87.7388272 and why because it increase percent so 88% now because you round.

Answer 2

Explanation:

In order to determine the equation, consider that any exponential growth equation can be written as follow:

`f(t)=A(1+r)^t`

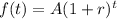
where,

f(t): amount of bacteria after t hours

A: initial amount of bacteria = 3

r: growth rate in decimal form = 0.15 (15%)

t: time in hours

By replacing the previous values into the expression for f(t) you get;

`f(t)=3(1+0.15)^t\\f(t)=3(1.15)^t`

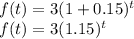
Hence, the answer is f(t) = 3(1.15)^t

Now, replace t = 13 to determine the amount of bacteria after 13 hours:

`f(13)=3(1.15)^13\\f(13)=18.46`

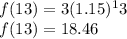
Hence, after 13 hours there are approximately 18 bacteria