Answer: Choice B. 3√2
This is the same as writing 3sqrt(2) or
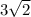
===========================================================
Reason:
For any complex number of the form
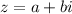 , the absolute value or magnitude of it is
, the absolute value or magnitude of it is
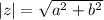
In this case, we have

So,
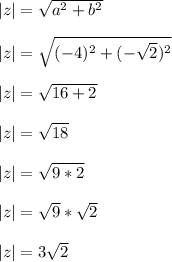
If we formed a segment with the endpoints
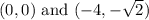 , then that segment will have length of the value mentioned above.
, then that segment will have length of the value mentioned above.
Side note: This formula or concept is related to the pythagorean theorem.