Question

Find the slope of a line parallel to -3x+7y=-15

Answer 1

`\boxed{\rm \: Slope = 3/7 \: x}`

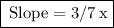
Explanation:

Given :

• 3x+7y=-15

To Find:

• The slope

Solution:

Well,to find out the slope of the line here, we'll need to re-write the fully solved equation into slope - intercept form.

`\boxed{ \rm \: y = mx = b}`

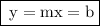
Here,

• m = slope
• b = y - intercept.

[Add 3x to both sides to the original equation:]

• 
  `\rm \: 7y = - 15 + 3x`

Divide each term in this equation by 7:

• 
  `\cfrac{7y}{7} = \cfrac{ - 15}{7} + \cfrac{3x}{7}`
• 
  `\rm \: y = \cfrac{ - 15}{7} + \cfrac{3x}{7}`

Now rewrite this equation into slope-intercept form.

• 
  `y = mx + b`

Plug values.

• 
  `y = \cfrac{3x}{7} - \cfrac{15}{7} = \cfrac{3}{7} x - \cfrac{15}{7}`

• > So , y - intercept is 15/7
• > Slope m is 3/7 x.

Hence,we can conclude:

• The slope of the line parallel to -3x+7y=-15 is 3/7 x.

`\rule{225pt}{2pt}`