Question

Write the equation of a line with the slope -3 and y-intercept of 5

O y = 5x + 3
O y = -5x + 3
O y = 5x - 3
O y = -3x + 5

Answer 1

`\fbox{y = -3x + 5}`

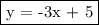
Explanation:

You are given the slope and the y-intercept of the line; so you can substitute these values into slope-intercept form:
`y=mx+b`;

• where
  `m= \ $slope = -3`
• and
  `y-$int = 5`

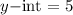
Plugging these values into slope-intercept form gives:

• 
  `y=(-3)x+(5)`

• 
  `y=-3x+5`

Another way to find the slope-intercept form of a line given the slope and a point:

We are given the slope and a point that the line passes through, so we can use the point-slope equation to find the slope-intercept form of the line.

The point that the line passes through is the y-intercept:
`(0,5)`.

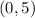Point-slope form:

• 
  `y-y_1=m(x-x_1)`

where
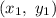`(x_1, \ y_1)` are the coordinates of the point that the line passes through and
`m= $ slope of the line.`

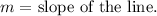
Substitute
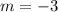`m=-3` and
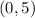`(0,5)` into the point-slope form equation.

• 
  `y-(5)=-3(x-(0))`

Simplify the equation on both sides.

• 
  `y-5=-3(x)`

Add 5 to both sides of the equation.

• 
  `y=-3x+5`

This is in slope-intercept form:
`y=mx+b`, so we are done.

The answer is
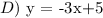`D) \ $y = -3x+5`.