Question

Nadia charges $5.50 an hour for babysitting. She babysits 17.50 hours the first week of the month and 21 hours the second week of the month.

Suppose Nadia raises her rate by $0.55 an hour. How many hours would she need to work to earn the same amount of money she made in the first two weeks of the month?

Answer 1

about 34 hours

Explanation:

Answer 2

35 hours.

Explanation:

To achieve an answer to this question, we'll have to set two expressions equal to each other.

Let's first start by calculating how much Nadia has made in the first two weeks of the month. We can do this by adding the amount of hours she works in the first and second week together:

`21+17.5`

`=38.5`

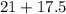
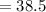
Let
`h` equal hours.

Set up your first expression:

`5.50h`

Let's go ahead and substitute 38.5 into the expression to see how much money she will make the first two weeks of the month at a rate of $5.50 an hour:

`5.50(38.5)`

`=211.75`

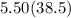
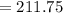
We are told that Nadia raises her rate by $0.55, so we'll need to add 0.55 to 5.50 in order to find her increased rate:

`5.50+0.55`

`=6.05`

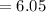
Set up your second expression:

`6.05h`

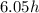
Now, set this equal to how much she made the first two weeks at a rate of $5.50 an hour:

`211.75=6.05h`

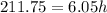
Divide both sides of the equation by the coefficient of
`h`, which is
`6.05`:

`35=h`

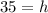
Therefore, it will take Nadia 35 hours to earn the same amount of money she made in the first two weeks of the month.

_

Check your work by substituting 35 for
`h` in the equation below:

`211.75=6.05h`

`211.75=6.05(35)`

`211.75=211.75`

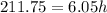
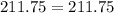
Since both sides of the equation are equal to each other, our answer is correct!