Question

please help me with this system of equations problem before I go insane the preferable solving methods would be through substitution or elimination

Answer 1

x=8, y=0, z=-3

Explanation:

Preferable is substitution because there is less room for mistakes but its long so here goes bare with me on this one :D

Name your equations

4x+2y-5z=47 (first eq)

x-2y+6z=-10 (second eq)

9x-7y-z=75 (third eq)

Lets take the easiest eq to isolate one variable lets take 2nd eq

`x-2y+6z=-10\\x=2y-6z-10`

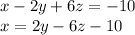
now this becomes our fourth eq

now again take the easiest eq to isolate another variable lets take the 3rd eq

`9x-7y-z=75\\9x-7y-75=z`

now this becomes our fifth eq

and now plug in our fifth eq in the fourth eq because we now have z in terms of x and y

`x=2y-6z-10\\x=2y-6(9x-7y-75)-10\\x=2y-54x+42y+450-10\\x+54x=2y+42y+450-10\\55x=44y+440\\\\x=(44y+440)/(55)`

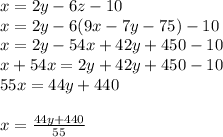
and now we got our sixth equation which is x only in terms of y.

now we plug in our sixth equation in our fifth eq to get z in terms of y only

`z=9x-7y-75\\\\z=9((44y+440)/(55)) -7y-75\\z=(396y+3960)/(55) -7y-75\\z=(396y+3960-385y-4125)/(55) \\z=(11y-165)/(55)`

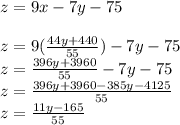
now we have our seventh eq and x &z in terms of just one variable y , now we put equation of z and x which is our sixth eq and seventh eq in our first eq.

`4x+2y-5z=47\\\\4((44y+440)/(55))+2y-5((11y-165)/(55)) =47\\\\(176y+1760)/(55) +2y-47=(11y-165)/(11) \\\\(176y+1760)/(55) -(11y-165)/(11) -47=-2y\\\\(176y+1760)/(55)-(y-15) -47=-2y\\\\(176y+1760)/(55) -y-32=-2y\\\\\\frac{176y+1760}{55}=-2y+y+32 \\\\176y+1760=55(-y+32)\\176y+1760=-55y+1760\\176y-55y=1760-1760\\121y=0\\y=0`

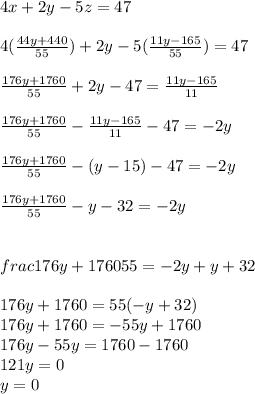
and now finally we got y=0 now we need the value of x and z, put the value of y=0 in our seventh eq (z equation)

`z=(11y-165)/(55) \\\\z=(11(0)-165)/(55) \\\\z=(-165)/(55)\\\\z=-3`

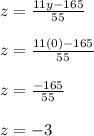
and now we put the value of y=0 in our sixth eq (x equation)

`x=(44y+440)/(55) \\\\x=(44(0)+440)/(55) \\\\x=(440)/(55) \\\\x=8`

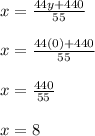
and now we got all the three values and hence the solution of the system of equation is

x=8, y=0, z=-3