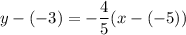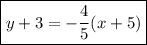Answer:
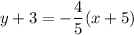
Explanation:
The point-slope form of the equation of a line is:
y-k=m(x-h)
Where m is the slope and (h,k) is a point through which the line passes.
We are required to find the equation of the line passing through the point (-5,-3) and parallel to the green line shown in the graph.
We need to find the slope of the green line. Once we have the slope, we will have the slope of our line since parallel lines have the same slope.
Suppose we know the line passes through points A(x1,y1) and B(x2,y2). The slope can be calculated with the equation:
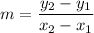
We can clearly identify the following points in the green line: (0,4) (5,0):
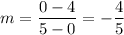
Now we have the slope and the point, the equation of the line is: