Answer:
The coordinates of its final image are
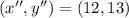 .
.
Explanation:
From Linear Algebra, we define reflection across the x-axis as:
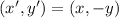 ,
,
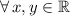
According to the statement of problem, the following operation of translation:
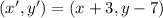 ,
,
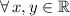
Where:
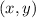 - Original point, dimensionless.
- Original point, dimensionless.
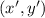 - Translated point, dimensionless.
- Translated point, dimensionless.
If we know that
 , we proceed to make the abovementioned operations:
, we proceed to make the abovementioned operations:
Translation
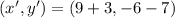

Reflection
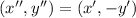
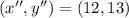
The coordinates of its final image are
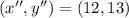 .
.