Question

If m27 = 55°, which of the following statements are true? Select all that apply.

2
3
4
5/6
8
A m26 = 55°
B
m25 = 135°
Cm21 + 24 = 250°
Dm21 + m26 = m 27+ m24

Answer 1

2, 3 , 5/6, b

Explanation:

Answer 2

The given statement requires determining the relationship between angles 1, 4, and 7. Statement C holds true, while statements A, B, and D are not necessarily true.

If (
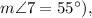`m\angle7=55^(\circ)),` which of the following statements are true? Select all that apply.

`A. (m\angle6=55^(\circ))\\B. (m\angle5=135^(\circ))`

`C. (m\angle1+m\angle4=250^(\circ))\\D. (m\angle1+m\angle6=m\angle7+m\angle4)$`

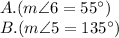
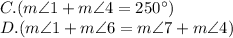
Answer:

Only statement C is true.

Solution:

Statement A:

Angle 6 and angle 7 are not alternate interior angles, so we cannot conclude that they have the same measure. Therefore, statement A is not necessarily true.

Statement B:

Angle 5 and angle 7 are corresponding angles, but we cannot conclude that they have supplementary measures based on the information given. Therefore, statement B is not necessarily true.

Statement C:

Angles 1 and 4 are supplementary angles, so we can conclude that
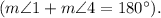`(m\angle1+m\angle4=180^(\circ)).` However, we also know that
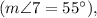`(m\angle7=55^(\circ)),`so we can conclude that
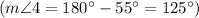`(m\angle4=180^(\circ)-55^(\circ)=125^(\circ))`. Therefore,
`(m\angle1+m\angle4=180^(\circ)+125^(\circ)=\boxed{250^(\circ)}).`

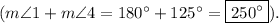
Statement D:

Statement D is a transitive property statement, but it is not necessarily true based on the information given. For example, if angles 1 and 6 are not supplementary angles, then statement D would not be true. Therefore, statement D is not necessarily true.

Conclusion:

Only statement C is true.