Question

An object launched at 65 degrees from the horizontal would have the same range

(distance travelled) as an object launched from? Write only the WHOLE number with
no units (example: 65)

Answer 1

An object launched from 65° will have the same range as an object launched from 25°

Step-by-step explanation:

The formula for the horizontal range, R, is given as follows;

`R = (v * sin(2\cdot \theta))/(g)`

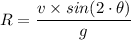
Therefore, given that sinθ increases from 0 to 1 for θ values from 0 to 90° and decreases from 1 to 0 for θ values from 90° to 180°, and that the values of sin(θ) are positive in the first and second quadrant, we have that for the given angle, θ = 65°, the range is therefore;

`R = (v * sin(2* 65 ^(\circ)))/(g) = (v * sin(130 ^(\circ)))/(g)`

The location of 130° = Second quadrant

A rotation of 130° in the counterclockwise is equivalent to a rotation of 50° in the clockwise direction

Therefore, we have sin(130°) = sin(50°)

Therefore, the range for 130°/2 = 65° is the same as the range for 50°/2 = 25° and an object launched from 65° will have the same range as an object launched from 25°.