Question

What is the solution for 3х + y = -5

Answer 1

`\tt Step-by-step~explanation:`

`\tt Solve~for~y:`

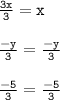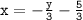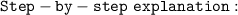
To solve for y, we have to move all of the terms that do not equal to y on one side, and let y be on the other side alone. Do this by subtracting 3x on both sides to cancel it out from the left side and bring it to the right.

`\tt 3x-3x+y=-5-3x\\y=-5-3x\\y=-3x-5`

`\tt Solve~for~x:`

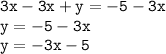
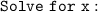
To solve for x, we will do the same thing we did to solve for y: move all the terms that do not equal to x to one side, and leave x on another side of the equation. We can do this by first subtracting y from both sides.

`\tt3x+y-y=-5-y\\3x=-y-5`

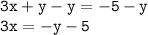
Then, we divide all terms by 3 to isolate the x.

`\tt (3x)/(3)=x\\\\ (-y)/(3)=(-y)/(3) \\\\(-5)/(3)=(-5)/(3)`

`\tt x=-(y)/(3) -(5)/(3)`

`\lare\boxed{\tt Our~final~answer:~y=-3x=5,~x=-(y)/(3)-(5)/(3) }`