I've attached a sketch of what I interpret the situation to be. It seems to me that you have to find the height of the projectile above the mountain's peak, assuming it actually does hit the ship on the other side. (Note that the sketch is not drawn to-scale. I don't mean to suggest that the projectile reaches its maximum height directly above the mountain.)
Compute the horizontal and vertical components of the velocity:
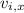 = (2.55 x 10² m/s) cos(72.4º) ≈ 77.1 m/s
= (2.55 x 10² m/s) cos(72.4º) ≈ 77.1 m/s
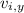 = (2.55 x 10² m/s) sin(72.4º) ≈ 243 m/s
= (2.55 x 10² m/s) sin(72.4º) ≈ 243 m/s
The projectile's horizontal and vertical positions at time t from its launching point are
x =
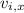 t
t
y =
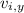 t - 1/2 (9.81 m/s²) t²
t - 1/2 (9.81 m/s²) t²
Find the time it takes for the projectile to travel the distance from the first ship to the mountain's peak:
2.47 x 10³ m = (77.1 m/s) t
t = (2.47 x 10³ m) / (77.1 m/s)
t ≈ 32.0 s
Find the vertical position at this time:
y = (243 m/s) (32.0 s) - 1/2 (9.81 m/s²) (32.0 s)²
y ≈ 2750 m = 2.75 x 10³ m
Take the difference of this height and the height of the mountain:
2.75 x 10³ m - 1.77 x 10³ m = 0.980 x 10³ m = 9.80 x 10² m