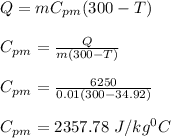Answer:
The final temperature of water is 34.92 ⁰C
The specific heat of the metal is 2357.78 J/kg⁰C
Step-by-step explanation:
Given;
mass of the hot metal, m = 10.0 g = 0.01 kg
temperature of the hot metal,
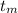 = 300 °C
= 300 °C
mass of water,
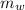 = 150 g = 0.15 kg
= 150 g = 0.15 kg
initial temperature of the water,
 = 25.0 °C
= 25.0 °C
heat lost by the hot metal = heat gained by water
Q = 6.25 kJ = 6250 J
let the final temperature of water = T
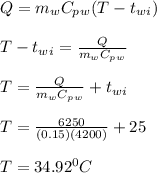
The final temperature of water is also the equilibrium temperature.
The specific heat of the metal is given by