Question

calculate the rate of change in your neighborhood population of squirrels based on the data from a june 2015

Answer 1

The question is incomplete. Here is the complete question.

Scenario: You are bored during quarantine. However, you have been observing a bird feeder in your backyard and wow... do there seem to be a lot of squirrels in your neighbourhood. You begin to wonder how many squirrels are actually in your neighbourhood and devise an experiment to track their population.

Part 1. Using the data below, estimate the population of squirrels in your neighbourhood as if you employed the Mark-and-Recapture method. Please be sure to include any units in your final answer.

#captured on 06/01/20 10

#captured on 06/30/20 6

#recaptured on 06/30 from 06/01 3

Part 2. Calculate the rate of change in your neighbourhood population of squirrels based on the data from a June 2015 report that indicated a population of 40 squirrels.

Part 3. Calculate the intrinsic growth rate (r) for this population of squirrels based on the data you have acquired so far.

Part 4. Interpretations: In 1-2 sentences, summarize what's happening here (e.g. is the population growing or shrinking or staying the same?) and propose one plausible explanation for this change.

Answer: Part 1: Population of 20 squirrels

Part 2: Rate of change 50%

Part 3: r = -0.1386 anos

Explanation: The Mark-and-Recapture method is a method to estimate a population when counting each individual is impractical. The method consists in capture a small population of individuals, mark them and released them back to the population. After a while, you catch another group and record the ones with the mark.

The calculations are made following this formula:

`N=(M*C)/(R)`

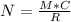
N is the estimated population

M is marked individuals

C is total number of captured individuals (with and without the mark) the second time

R is recaptured individuals with the mark.

Part 1: Population of squirrels will be:

`N=(10*6)/(3)`

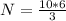
N = 20

Population of squirrels in 2020 is 20 squirrels.

Part 2: Rate of change is calculated by the change in the population divided by the original population:

rate =
`(20-40)/(40)`

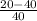
rate = - 0.5 or 50%

Part 3: The model for a population growth is exponential:

`N=N_(0)e^(rt)`

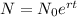
N is population at that moment

N₀ is initial population

r is growth rate

t is period of time

Growth rate will be:

`N=N_(0)e^(rt)`

`20=40e^(5r)`

`e^(5r)=0.5`

`5r=ln(0.5)`

`r=(ln0.5)/(5)`

`r=-0.1386`

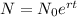
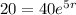
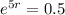
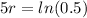
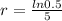
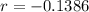
Growth rate (r) for the population of squirrels after 5 years is
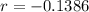`r=-0.1386` years.

Part 4: The growth rate has a negative sign, which means population is decreasing along the 5 years, so population is shrinking.

One possible explanation is the environment the population are in is lacking the squirrels primary need, i.e., squirrels' food source is diminishing, causing the population to decrease.