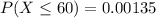Answer:
The value is
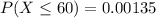
Explanation:
From the question we are told that
The mean is

The standard deviation is
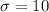
Generally 1 hours = 60 minutes
Generally the probability that the exam will be completed in one hour or less is
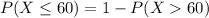
Here

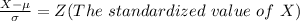
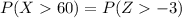
From the z -distribution table the probability of ( Z> -3 )
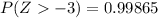
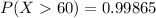
=>
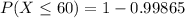
=>