Answer:
C. Increasing the vertical height from which the ball is thrown.
Step-by-step explanation:
In this case, we understand that ball experiments a parabolical motion, which is the combination of horizontal uniform motion and vertical uniform accelerated motion, due to gravity. Equations of motion for the ball are described below:
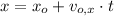 (Eq. 1)
(Eq. 1)
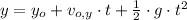 (Eq. 2)
(Eq. 2)
Where:
 ,
,
 - Initial and final horizontal positions, measured in meters.
- Initial and final horizontal positions, measured in meters.
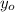 ,
,
 - Initial and final vertical positions, measured in meters.
- Initial and final vertical positions, measured in meters.
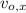 ,
,
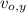 - Initial horizontal and vertical velocities, measured in meters per second.
- Initial horizontal and vertical velocities, measured in meters per second.
 - Gravitational acceleration, measured in meters per second.
- Gravitational acceleration, measured in meters per second.
 - Time, measured in seconds.
- Time, measured in seconds.
Now we get (Eq. 2) and solve the expression for the time:
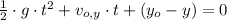
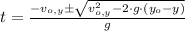
If
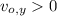 ,
,
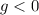 and
and
 , then maximum time occurs when:
, then maximum time occurs when:
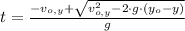
And,
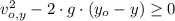 .
.
If
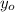 is increased, then
is increased, then
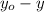 goes closer to zero and
goes closer to zero and
 becomes greater and time increased. Hence, we conclude that correct answer is C.
becomes greater and time increased. Hence, we conclude that correct answer is C.