Question

What is the length of the hypotenuse?If necessary,round to the nearest tenth

Answer 1

85 yd

Explanation:

We know that

`\pmb{\bf H^2=P^2+B^2}`

Here,

H = c, P = 75 yd, B = 40 yd

`\begin{gathered} \: \sf \implies \: {c }^(2) = (75) {}^(2) + {(40)}^(2) \\ \sf \implies {c}^(2) = 5625 + 1600 \\ \sf \implies \: {c}^(2) = 7225 \\ \sf \implies \: c = √(7225) \\ \sf \implies \: c = 85 \: yd \end{gathered}`

Answer 2

Answer: 85

Work Shown:

`a^2 + b^2 = c^2\\\\40^2 + 75^2 = c^2\\\\1600 + 5625 = c^2\\\\7225 = c^2\\\\c^2 = 7225\\\\c = √(7225)\\\\c = 85\\\\`

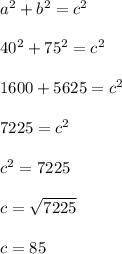
I used the pythagorean theorem with a = 40 and b = 75. The order of the 'a' and b doesn't matter, as long as c is the largest side.

The 40-75-85 pythagorean triple is the scaled up version of the 8-15-17 triple (multiply each piece by 5).