Question

Assume that the weights of quarters are approximately normally distributed with a mean of 5.67 g and a standard deviation of 0.07 g. A vending machine will only accept coins weighing between 5.48 g and 5.82 g. What percentage of legal quarters will be rejected

Answer 1

Answer: 1.94%

Explanation:

Given: The weights of quarters are approximately normally distributed with
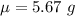`\mu=5.67\ g` and
`\sigma=0.07\ g`.

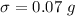Machine will only accept coins weighing between 5.48 g and 5.82 g.

Let X be the weight of quarters.

The probability that legal quarters will be rejected = P(X<5.48)+P(X>5.82)

`=P((X-\mu)/(\sigma)<(5.48-5.67)/(0.07))+P((X-\mu)/(\sigma)>(5.82-5.67)/(0.07))\\\\=P(Z<-2.714)+P(Z>2.142)\ \ \ \[Z=(X-\mu)/(\sigma)]\\\\=(1-P(Z<2.714))+(1-P(Z<2.142))\ \ \ \ [P(Z<-z)=1-P(Z<z)=P(Z>z)]\\\\=(1- 0.9967)+(1-0.9839)\ \ \ \ [\text{By p-value table}]\\\\= 0.0033+0.0161=0.0194=1.94\%`

Hence, the percentage of legal quarters will be rejected = 1.94%