Answer:
The correct answer -
1. volume of the plasmid: 2 ml
2. insert needed = 100 mg
Step-by-step explanation:
Calculating the inserted by the formula:
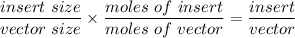
for a mormal vector size using 50 mg of vector DNA per ligation reaction.
take x as required insert:
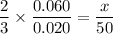
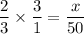
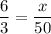
3x = 300
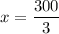
x = 100 mg
Volume of plasmid vector is :
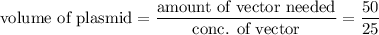
volume of plamid vector = 2 ml.