Answer:
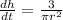 meters per minute
meters per minute
Explanation:
Volume of a cylinder is given by the formula,
V = πr²h
Where r = radius of the cylindrical tank
h = height of the tank
Water is filling in this tank = 3 cubic meters per second
Derivative of volume will show the change in volume of the water in the tank.
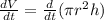
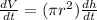
By putting
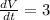 in the expression,
in the expression,
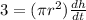 [Since 'r' is a constant]
[Since 'r' is a constant]
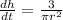
Therefore, rate of increase in height of the water level will be represented by,
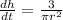 meters per minute
meters per minute