Question

Consider two current-carrying circular loops. Both are made from one strand of wire and both carry the same current, but one has twice the radius of the other. If the magnetic field strength at the center of the smaller loop is B, what is the magnetic field strength at the center of the larger loop

Answer 1

Step-by-step explanation:

The magnetic field at the center of a current-carrying circular loop is given by :

`B=(\mu_o I)/(2r)`

Where, I is current and r is radius of loop

We have, two current-carrying circular loops. Both are made from one strand of wire and both carry the same current, but one has twice the radius of the other.

For smaller loop, the magnetic field is B (with radius r)

For larger loop, let the magnetic field be B' (with radius r', r'=2r). So,

`B'=(\mu_o I)/(2r')\\\\B'=(\mu_o I)/(2(2r))\\\\B'=(1)/(2)* (\mu_o I)/(2r)\\\\B'=(1)/(2)B`

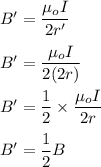
Hence, the magnetic field strength at the center of the larger loop is half of the magnetic field strength at the center of the smaller loop.