Answer: 0.376
Explanation:
Given: X is a normal random variable, with its mean
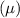 of 3 and its standard deviation
of 3 and its standard deviation
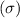 of 2.
of 2.
Sample size : n= 10
The probability that the sample mean of X exceeds 3.2 will be :
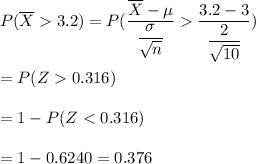
Hence, the probability that the sample mean of X exceeds 3.2= 0.376