♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
From left to right for the tables :
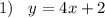
And
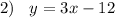
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️
To find the solution we need to take equal above equations .

Subtract sides 3x

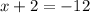
Subtract sides 2
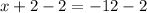
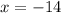
Thus the x-coordinate of the solution must be -14 which is just in the last option.
Thus the correct answer is the last one.
Done...
♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️