Question

if x=-3 is the only x-incercept of the graph of a quadratic equation which statement best describes the discrinant of the equation

Answer 1

The discriminant must be zero.

Explanation:

Quadratic Equation

The standard representation of a quadratic function is:

`f(x)=ax^2+bx+c`

where a,b, and c are constants.

The zeros, roots, or x-intercepts can be found by solving the equation:

`ax^2+bx+c=0`

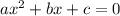
We can use the quadratic formula to find the roots:

`\displaystyle x=(-b\pm √(b^2-4ac))/(2a)`

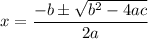
Note this formula gives us two different roots if the square root is non-zero.

The only way there can be only one x-intercept is because the square root is zero.

If the square root is zero, then

`b^2-4ac =0`

The expression is called the discriminant.

Thus, if x=-3 is the only x-intercept of the graph of a quadratic function, then the discriminant must be zero.