Question

One line passes through the points (-7, 4) and (5, -4). Another line passes through points (-7, -4) and (2, 2). Are the lines parallel, perpendicular, or neither?

Answer 1

♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️

We just need to find the slope of both lines.

_________________________________

IF their slopes are same they are parallel.

++++++++++++++++++++++++++++++++++++

IF their slopes are negative and inverse with each other , they are perpendicular ,

thus when we multiply them the answer must equals - 1 .

Which means :

slope ( L 1 ) × slope ( L 2 ) = - 1

++++++++++++++++++++++++++++++++++++

And Neither when none of above phrases happened.

_________________________________

LINE (1)

A = ( - 7 , 4 ) & B = ( 5 , - 4 )

We have following equation to find the slope using two points :

`slope = (y( B) - y( A) )/(x( B) - x( A) ) \\`

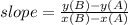
Now just need to put coordinates in the above equation :

`slope = ( - 4 - 4)/(5 - ( - 7)) \\`

`slope = ( - 8)/(5 + 7) \\`

`slope = - (8)/(12) \\`

`slope = - (2)/( 3) \\`

##############################

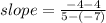
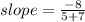
LINE (2)

C = ( - 7 , - 4 ) & D = ( 2 , 2 )

`slope = (y( D) - y( C) )/(x( D) - x( C) ) \\`

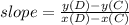
Put the coordinates.

`slope = (2 - ( - 4))/(2 - ( - 7)) \\`

`slope = (2 + 4)/(2 + 7) \\`

`slope = (6)/(9) \\`

`slope = (2)/(3) \\`

_________________________________

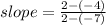
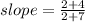
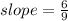
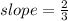
CHECK ;

`- (2)/(3) ≠(2)/(3) \\`

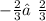
Thus they are not parallel .

`- (2)/( 3) * (2)/(3) = - (4)/(9) ≠ - 1 \\`

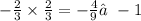
Thus they are not perpendicular.

So Neither.

♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️

Done...

♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️