Question

What is the perimeter of the parallelogram

Answer 1

The perimeter of the parallelogram is 36 units.

To find the perimeter of the parallelogram, we need to sum the lengths of all its sides. In a parallelogram, opposite sides are equal in length. If we can identify the lengths of the adjacent sides, we can simply double the sum of these lengths to find the perimeter.

Here's how we can calculate it step by step:

1. Measure the length of one horizontal side by counting the number of squares it spans.

2. Measure the length of one vertical side in the same way.

3. Calculate the perimeter using the formula
`\( P = 2 * (\text{length} + \text{width}) \).`

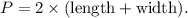
From the given graph we can calculate the lengths of the sides of the parallelogram:

- The shorter side is 5 units.

- The longer side can be found using the Pythagorean theorem since it forms a right triangle with the height of the parallelogram and the projected length on the x-axis. This is given by
`\( √((12)^2 + (5)^2) \).`

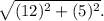
Let's calculate the length of the longer side:

`\[ \text{Longer side} = √(12^2 + 5^2) \]`

`\[ \text{Longer side} = √(144 + 25) \]`

`\[ \text{Longer side} = √(169) \]`

`\[ \text{Longer side} = 13 \text{ units} \]`

Now, to find the perimeter of the parallelogram
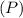`(\( P \))`, we'll use the formula:

`\[ P = 2 * (\text{shorter side} + \text{longer side}) \]`

`\[ P = 2 * (5 + 13) \]`

`\[ P = 2 * 18 \]`

`\[ P = 36 \text{ units} \]`

Therefore, the perimeter of the parallelogram is 36 units.

Answer 2

34

Explanation:

p= l+l+w+w

5+5+12+12=

10+24=

34