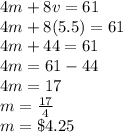Answer:
A movie costs $4.25 and a video game $5.5.
Explanation:
Step 1: Form the equations.
Let m be the price of a movie and v the price of the video game.
First equation: One month Jessica rented 4 movies and 8 video games for a total of $61.
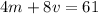
Second equation: The next month she rented 2 movies and 3 video games for a total of $25.
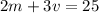
Step 2: Solve the system of equations.
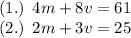
I'm going to solve them by elimination. I'll multiply the second equation with two so I get 4m.

Now I'm going to subtract the second equation from the first.
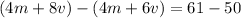
And solve.
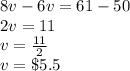
Now let's insert v back in second equation to get m (nicer numbers, you can insert in first too if you want).