Question

The volume of a right cone is 3000π units^3. If its radius measures 15 units, find its height.

Answer 1

• 40 units

Explanation:

In the question, it is given that a right cone has a radius of 15 units and volume of 3000π units³ and we have to find the height of the cone.

`\:`

To Find the height of the cone, we must know this formula :

`\\{\longrightarrow{ \qquad{\underline{\boxed {\pmb{\frak { (1)/(3) \: \pi {r}^(2)h ={ Volume_((cone) )}}}}}}}} \\ \\`

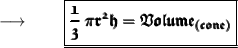
Where,

• r refers to the radius of the cone.

• h refers to the height of the cone.

Now, we will substitute the values in the formula :

`\\ {\longrightarrow{ \qquad{{ {\pmb{\sf { (1)/(3) * \pi * {(15)}^(2) * h = 3000 \pi}}}}}}} \\ \\`

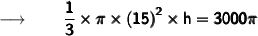
Cancelling π from both sides we get :

`\\ {\longrightarrow{ \qquad{{ {\pmb{\sf { (1)/(3) * \cancel\pi * {(15)}^(2) * h = 3000 \cancel\pi}}}}}}} \\ \\`

`\\ {\longrightarrow{ \qquad{{ {\pmb{\sf { (1)/(3) * 225 * h = 3000}}}}}}} \\ \\`

`\\ {\longrightarrow{ \qquad{{ {\pmb{\sf { (225)/(3) * h = 3000}}}}}}} \\ \\`

`\\ {\longrightarrow{ \qquad{{ {\pmb{\sf 75 * h = 3000}}}}}} \\ \\`

`\\ {\longrightarrow{ \qquad{{ {\pmb{\sf h = (3000)/(75) }}}}}} \\ \\`

`\\{\longrightarrow{ \qquad{\underline{\boxed {\pmb{\frak { h =40 }}}}}}} \\ \\`

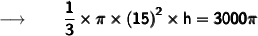
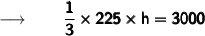
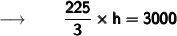
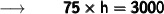
Therefore,

• The height of the cone is 40 units .