Question

Complete all parts of the problem.

Answer 1

(a)

`\bigcup\limits_(i=1)^7R_i=R_1=\boxed{[1,2]}`

(b)

`\bigcap\limits_(i=1)^7R_i=R_7=\boxed{\left[1,\frac87\right]}`

(c) No, because no two sets are disjoint. Why? Each of the
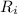`R_i` contain the endpoint 1, so at the very least,
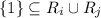`\{1\}\subseteq R_i\cup R_j` for
`i\\eq j`.

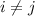(d)

`\bigcup\limits_(i=1)^nR_i=R_1=\boxed{[1,2]}`

(e)

`\bigcap\limits_(i=1)^nR_i=R_n=\boxed{\left[1,\frac{n+1}n\right]}`

(f)

`\bigcup\limits_(i=1)^\infty R_i=R_1=\boxed{[1,2]}`

because as i gets larger, the set
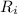`R_i` gets smaller. The infinite union will be equivalent to the largest set in the family of sets.

(g)

`\bigcap\limits_(i=1)^\infty R_i=\boxed{\{1\}}`

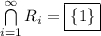
because 1 + 1/n converges to 1 as n goes to infinity, so
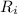`R_i` converges to the singleton set {1} as i goes to infinity.