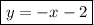Answer:
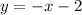
Explanation:
Slope-Intercept form of the line
Any given line with slope m and y-intercept b can be written as:
y=mx+b
We need to find the equation of a line parallel to
2x + 2y = 6
Dividing by 2:
x + y = 3
Solving for y:
y = -x + 3
Comparing with the slope-intercept form of the line:
m = -1
Parallel lines have the same slope, thus the required line must have a slope m = -1.
Since we have a point through which the line passes, we use the point-slope form:
y - k = m ( x - h )
Where (h,k) is the point.
The required equation of the line is:
y - (-5) = -1 (x - 3)
Operating:
y + 5 = -x + 3
Solving for y: