Answer:
The wavelength of light (in nm) of the spectral line of Hydrogen where an electron falls from the 6th Bohr orbit to the 3rd Bohr orbit is 1090nm
Step-by-step explanation:
We know that , the wavelength of the light is calculated by Rydberg's formula-
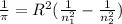
![[n_2>n_1]](https://img.qammunity.org/2021/formulas/chemistry/college/5taevhkhqrowm1vyc3nl432a70u0pnb6nz.png)
Here , R = Rydberg's constant
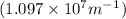
Z = atomic number (for hydrogen , Z= 1)
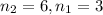
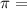 wavelength of light
wavelength of light
Now , putting the values in the Rydberg's formula ,
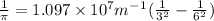
=
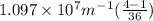
=
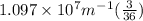
=
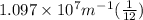
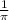 =
=
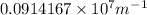
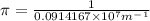
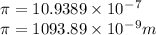
=1090nm
Hence , the wavelength of the light is 1090nm,, that is option D is correct.