Question

Which equation has solutions of 6 and -6?

x^2 - 12x + 36 = 0
x^2 + 12x - 36 = 0
x²+36=0
x^2- 36 = 0

Answer 1

♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️

Let's solve all of them to see :

_________________________________

`{x}^(2) - 12x + 36 = 0`

`({x - 6})^(2 ) = 0`

`x - 6 = 0`

`x = 6`

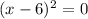
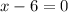
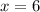
There's only one solution , thus it's not what we want.

_________________________________

`{x}^(2) + 12x - 36 = 0`

`(x - ( - 6 + 6 √(2)) \: )(x - ( - 6 - 6 √(2)) \: ) = 0 \\`

`x - ( - 6 + 6 √(2) ) = 0`

`x = - 6 + 6 √(2)`

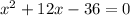
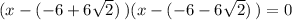
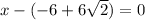
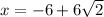
And

`x - ( - 6 - 6 √(2) ) = 0`

`x = - 6 - 6 √(2)`

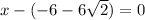
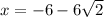
There are two solutions but none of them is what we want .

_________________________________

`{x}^(2) + 36 = 0`

`{x}^(2) = - 36`

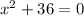
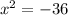
There's no solution because square of any number is greater than or equal zero

which means :

`{x}^(2) \geqslant 0`

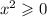
Thus x² never can be a negative number.

_________________________________

`{x}^(2) - 36 = 0`

`(x - 6)(x + 6) = 0`

`x - 6 = 0`

`x = 6`

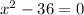
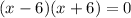
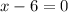
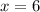
And

`x + 6 = 0`

`x = - 6`

These are exactly the solutions what we want ;

Thus the correct answer is the last one.

♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️♥️