Question

HELP! A line goes through the points (8,10) and .

What is the slope of the line? Show your work

Write the equation of the line in point-slope form. Show your work

Write the equation of the line in slope-intercept form. Show your work.


I will give y'all 50 points please answer and show your work! Please keep in mind I am not afraid to report someone.

Answer 1

3/5

Explanation:

did the test

Answer 2

slope is
`(3)/(5)` ; slope-intercept form is y =
`(3)/(5)` x +
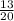`(13)/(20)` ; point-slope form is 4 - 10 =
`(3)/(5)` (-2 - 8)

Explanation:

first, we find the slope by using our points (8,10) and (-2,4)

to do so, you use the expression
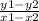`(y1 - y2)/(x1 - x2\\)` where (8,10) is point 1 and (-2,4) is point 2

this results in
`(10-4)/(8--2)`

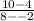
10-4 is 6 and 8--2 is 10

which results in the slope of
`(3)/(5)`

now that we have the slope, we can solve for the y-intercept using the slope-intercept formula [y = mx +b]

we choose a point [im using (8,10)] and but the values in for x and y in the equation, which gives us 10 = 3/5 (8) + b , and solve for b

to solve for b, we start by dividing both sides by 8, resulting in 5/4 = 3/5 +b

then, subtract 3/5 from 5/4, resulting in 13/20 = b

To check the work, we use slope-intercept formula again [yeyyy]

y = 3/5x + 13/20 ; 4 = 3/5 (-2) + 13/20

i used my calculator to check, it's correct

SO: the slope-intercept form of the equation is y =
`(3)/(5)` x +
`(13)/(20)`

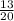
now we get to do the point-slope formula [yeyyyyyyyyyyy!!!]

point-slope formula is y - y1 = m (x - x1)

the slope [m] is
`(3)/(5)`

and we use any given point [im using (8,10) again, but any point should technically be correct] for y1 and x1

inputting our values, we get y - 10 = 3/5 (x - 8)

now, you use any other point for x and y to check the work

4 - 10 = 3/5 (-2 - 8)

-2 - 8 is -10, and 3/5 times -10 is -6, which is equal to 4 - 10