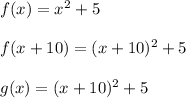Question

Consider the following function f(x) = x² + 5.

Part A: Write a function, in vertex form, that shifts f(x) right 3 units.
Part B: Write a function, in vertex form, that shifts f(x) left 10 units.

Answer 1

Part A

To shift the curve 3 units to the right, we'll replace x with x-3. What this does is move the xy axis 3 units to the left. If we held the curve in place as the axis moves, then it gives the illusion the curve is moving 3 units to the right.

`f(x) = x^2 + 5\\\\f(x-3) = (x-3)^2 + 5\\\\g(x) = (x-3)^2 + 5\\\\`

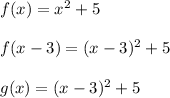
Do not expand out the (x-3)^2 term, because you want to keep the function in vertex form. The old vertex of (0,5) moves three units to the right to arrive at (3,5)

Answer:
`g(x) = (x-3)^2 + 5`

==============================================================

Part B

We use the same idea as before. This time we're moving the curve 10 units to the left, so we'll replace x with x+10

`f(x) = x^2 + 5\\\\f(x+10) = (x+10)^2 + 5\\\\g(x) = (x+10)^2 + 5\\\\`