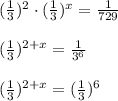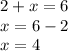Question

Find the value of x in the equation without evaluating the power

Answer 1

a) x = 3

b) x = 4

Explanation:

Use the Exponential Power Rule.

`a^x * a^y = a^(x+y)`

Also covert the term on the right to the same base as on the left.

If you are allowed to have calculator do
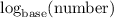`\log_{\text{base}} (\text{number})` to get the exponent. For example
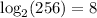`\log_(2) (256) = 8`, that means
`256 = 2^8.`

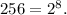
Without calculator you can divide with base untill you have it fully factored, then count. For example:

256/2 = 128
128/2 = 64
64/2 = 32
32/2 = 16
16/2 = 8
8/2 = 4
4/2 = 2
2/2 = 1

We had to divide with base two 8 times so 256 = 2⁸.

a)

`2^5 \cdot 2^x = 256\\2^(5+x) = 2^8`

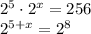
Now that we have same base we can equate the exponents!

`5 + x = 8\\x = 8 - 5\\x = 3`

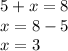
b)

`((1)/(3))^2 \cdot ((1)/(3))^x = (1)/(729)\\\\((1)/(3))^(2+x) = (1)/(3^6)\\\\((1)/(3))^(2+x) = ((1)/(3))^6`

`2 + x = 6\\x = 6 - 2\\x = 4`

Answer 2

See below

Explanation:

2 ^(5+x) = 2^8 (because 256 = 2^8)

equate the exponents 5+x = 8 then x = 3

1/3 ^(2+x) = 1 / 3^ 6 (because 729 = 3^6 )

equate the exponents 2+ x = 6 then x = 4