Question

Help me with this extremely hard differentiation question , [Scroll] >>


`\huge(d)/(dx)[\sum_(n=0)^(∞)[(\frac{(-1) ^ {n}}{(2n+1)!})((1)/(1+e^(x)))^(2n+1)] ]` ​

Answer 1

`f'(x)=\displaystyle -(e^x)/((1+e^x)^2)\cos\biggr((1)/(1+e^x)\biggr)`

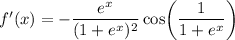
Explanation:

Recall the power series
`\sin(x)=\displaystyle \sum\limits^\infty_(n=0)(-1)^n(x^(2n+1))/((2n+1)!)`.

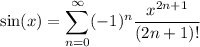In this case,
`x` is replaced with
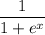`\displaystyle (1)/(1+e^x)`, so our power series actually works out to be
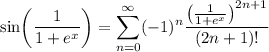`\displaystyle \sin\biggr((1)/(1+e^x)\biggr) =\sum\limits^\infty_(n=0)(-1)^n(\bigr((1)/(1+e^x)\bigr)^(2n+1))/((2n+1)!)`! Amazing, huh?

Now, we find the derivative of the function by using the chain rule:

`\displaystyle (d)/(dx)\sin\biggr((1)/(1+e^x)\biggr)=(d)/(dx)\biggr((1)/(1+e^x)\biggr)*\cos\biggr((1)/(1+e^x)\biggr)=-(e^x)/((1+e^x)^2)\cos\biggr((1)/(1+e^x)\biggr)`

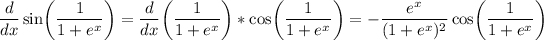
You didn't specify if you just wanted the derivative of the series to be a function or a series, so I'm going to assume you want the function. Let me know if there's more to your problem.