Answer:
a) x = 7.5
b) 15, 11.5, 8
c) -3.5
Explanation:
As there is a common difference between consecutive terms of an arithmetic progression, then:

Given:
Therefore:
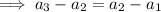
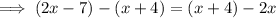

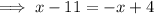

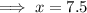
Inputting the found value of x into the term expressions to find the three terms of the arithmetic progression:
The common difference (d) is the difference between each consecutive term. To find the common difference, subtract one term from the next term:
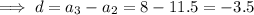

Therefore, the common difference is -3.5