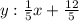Question

Finding the area of a triangle is straightforward if you know the length of the base and the height of the triangle. But is it possible to find the area of a triangle if you know only the coordinates of its vertices? In this task, you’ll find out. Consider ΔABC, whose vertices are A(2, 1), B(3, 3), and C(1, 6); let line segment AC represent the base of the triangle.

Part A
Find the equation of the line passing through B and perpendicular to AC .

Answer 1

Yes it's possible through matrix

Let's find out the area formula for our vertices

That's

`\\ \rm\Rrightarrow \left|\begin{array}{ccc}\rm 2&\rm 1&\rm 1\\ \rm 3&\rm 3&\rm 1\\ \rm 1&\rm 6&\rm 1\end{array}\right|`

The determinant values modulus is the area

Slope of AC

• m=6-1/1-2=-5

Perpendicular lines have slopes negative reciprocal to each other

• Slope of line B to AC =1/5

So

Equation in point slope

• y-3=1/5(x-3)
• y=1/5x-3/5+3
• y=1/5x+12/5

Answer 2

`y : (1)/(5) x + (12)/(5)`

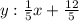
Explanation:

the slope of the line AC :

`(6-1)/(1-2) = (5)/(-1) =-5`

Let y : mx + p be the equation of the line D passing through B and perpendicular to AC.

Where m is the slope and p is the y value of the y intercept point.

The line D is perpendicular to AC means the product of their slopes is −1

Therefore

(−5) × m = −1

Then

`m=(-1)/(-5) =(1)/(5)`

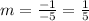
We obtain, the equation of D is :

`y : (1)/(5) x + p`

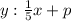
At this point ,we still need the value of p to get the full equation of D.

B(3, 3)∈ D

`3=(1)/(5) \left( 3\right) +p`

`\Longleftrightarrow p=3-(3)/(5) =(12)/(5) =2.4`

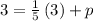
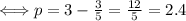
thus , the equation of D is :

`y : (1)/(5) x + (12)/(5)`