Answer:
(
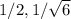 ),(-1/2,
),(-1/2,
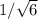 ),(-1/2,
),(-1/2,
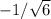 ) and
) and
(
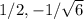 )
)
Explanation:
We are given that
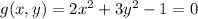
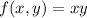
Using Lagrange's multipliers
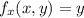
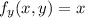
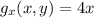
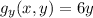
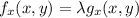
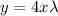
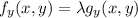
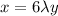
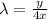 ...(1)
...(1)
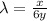 ...(2)
...(2)
Equation (1) divided by (2) Then we get
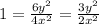
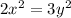
Substitute the values in g(x,y)
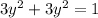
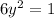
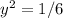
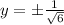
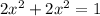
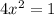
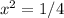
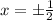
Therefore, the points on the ellipse are
(
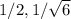 ),(-1/2,
),(-1/2,
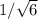 ),(-1/2,
),(-1/2,
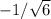 ) and
) and
(
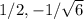 )
)