Answer:
(0, 7, 9)
Explanation:
The direction vector (a, b, c) is given by B - A
(a, b, c) = (−1, 5, 6) - (-3, 1, 0) = (2, 4, 6)
(a, b, c) = (2, 4, 6)
Let us use point A as
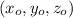 , therefore (-3, 1, 0) =
, therefore (-3, 1, 0) =
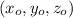
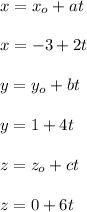
Substituting the value of x, y and z into the plane equation:
2x + y − z + 2 = 0
2(-3+2t) + (1 + 4t) - (6t) + 2 = 0
-6 + 4t + 1 + 4t - 6t + 2 = 0
2t -3 = 0
2t = 3
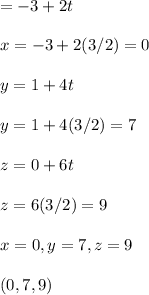
t = 3/2