Complete Question
The equation you found in Part D may be factored to give(E2−E1)(E2+E1)=p22c2−p21c2.Consider the term E2+E1. Since we are looking at the "everyday" limit of relativity, where speed is far lower than the speed of light, the kinetic energy will be negligible compared to the rest energy. Using this approximation, find the value of E2+E1
Answer:
The value is
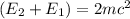
Step-by-step explanation:
Generally in the question we are given this equation

and the objective is to obtain the value of
 in terms of m and c
in terms of m and c
Generally kinetic energy is mathematically represented as
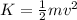
=>
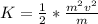
recall that momentum is mathematically represented as
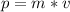
Hence
=>
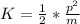
Hence
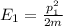 and
and
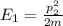
So
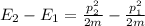
=>
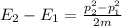
So from the given equation
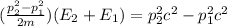
=>
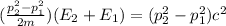
=>

=>